Planteamiento

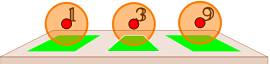
En la ventana de la derecha tienes tres fichas con los números 9, 3 y 1. Se trata de acomodar las fichas dentro de las casillas rojas de manera que el número resultante sea un número primo.

Para mover las fichas selecciona el punto rojo y arrastra con el mouse. Las casillas rojas se vuelven azules al detectar el movimiento de las fichas y se vuelven verdes al obtener la respuesta correcta.

Reflexión

Se dice que un número es primo si cumple con las características de ser mayor que 1 y solo poderse dividir entre sí mismo y entre 1, es decir, que ningún otro número lo puede dividir.

Los números primos son la base para construir todos los demás números naturales, por lo tanto, cualquier número natural es producto de números primos.

En efecto, el Teorema fundamental de la aritmética establece que:

Todo número natural n > 1 puede ser representado de manera única (excepto orden) como un producto de potencias de números primos.

Intenta y tal vez te surja la idea de cómo solucionar el problema.

Sugerencias

Forma combinaciones con los tres números y busca sus posibles divisores, recuerda lo aprendido en la reflexión.

Observa los núméros en las fichas y haz todas las combinaciones posibles: 913, 931, 139, ... ¿cuántas tienes?

Aplica en todos los casos, tu definición de primo o tus reglas de divisibilidad.

Puedes dividir cada combinación con los primeros numeros primos: 2, 3, 5, 7, 11, etc. Si se obtiene una división exacta, entonces el número no es primo.

Si el cociente es menor que el divisor, puedes dejar de dividir y afirmar que el número es primo.

Si se te dificulta construir una idea, puedes solicitar una Sugerencia.

Solución

De las posibles combinaciones con las fichas se forman dos números que son primos, el 139 y el 193.

Al empezar a dividir el número 139 con los primeros numeros primos, observamos lo siguiente:

139 no es divisible por 2 pues se obtiene un cociente de 69.5
139 no es divisible por 3 pues se obtiene un cociente de 46.3...
139 no es divisible por 5 pues se obtiene un cociente de 27.8
139 no es divisible por 7 pues se obtiene un cociente de 19.8...
139 no es divisible por 11 pues se obtiene un cociente de 12.6...
139 no es divisible por 13 pues se obtiene un cociente de 10.6...

Hasta ahí paramos la división, ya que el último cociente obtenido es menor al divisor, por lo tanto 139 es primo.

Prueba hacer lo mismo con el número 193 para comprobar que es un número primo.

¿Podrías encontra otra combinación que forme un número primo?